Blackjack Lucky Lucky Odds
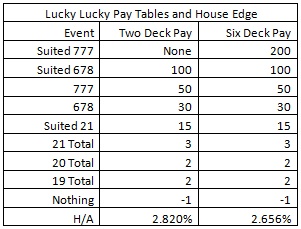
The minimum bet for this game is $10, whereas the maximum amount is $500. Lucky Lucky Blackjack Side Bet. In addition to the standard Blackjack gameplay, players at Cache Creek can spark things up by placing an extra wager on one of the most interesting Blackjack side bets, known as Lucky Lucky Blackjack. Game Description. Lucky Lucky Blackjack is a traditional blackjack game that allows you to play up to five hands simultaneously but with the addition of a side bet that could see you win a huge payout. The Lucky Lucky side bet is a bet on the first two cards in a hand and the dealer's face-up card forming one of eight winning combinations and it can payout up to 200:1. By the way, if you’re curious about the side bet, Lucky Lucky comes with a house edge of about 5.86%. That’s hardly outrageous in the world of casino bonus bets, but it’s not great, either; even if you enjoy this option, you should probably either play it for much less than your blackjack wagers, or just once in a while for a change of pace. Canterbury Basic Training teaches you how to play two Blackjack side bets, TriLux Bonus and Lucky Lucky. Lucky Lucky Blackjack Side Bet. Lucky Lucky Side bet is used in some variations that concerns first player two cards and dealer up card. All three cards may win as an overall total and a combination of some cards. Any total 19 and 20 pays 2 to 1; Unsuited 21 pays 15 to 1; Suited 21 pays 15 to 1; Unsuited 678 pays 30 to 1; Unsuited 777 pays 50 to 1; Suited 678 – 100 to 1 and Suited 777 pay 200 to 1.

Thank you so much for the help to my previous question.
Has any research been done on the 'Lucky Lucky' side bet in BJ? For those that have never heard of it, it is a side bet anywhere from $1-25 and these are the payouts:
Suited 777: 200 to 1
Suited 678: 100 to 1
777: 50 to 1
678: 30 to 1
Suited 21: 15 to 1
21 Total: 3 to 1
20 Total: 2 to 1
19 Total: 2 to 1
18 Total or less: Loss
I see a lot of sheep players betting 'Lucky Lucky', and for some I realize that they are winning more at their side bet than their regular BJ bet. Others consistently lose hopeful of getting even the lowest payout.
Just a few days ago I hit a suited 777 and was the talk of the house. Of course, I didn't bet, but it got me thinking.... could this little side bet be beatable? I use Hi-Lo, at what count, if any, could I have an edge on this game? Any information on this side bet would be great!
I have done some research but haven't got many results on the forum and search engines, but I am very curious to know at what count this could make some extra $$ and just any insight on this at all would be greatly appreciated.
Or is this side bet really just based on luck?
-clouds
Assuming an average amount of hands dealt per hour (it was about 4 people at the table if that matters), what are the odds of actually getting that Lucky Lucky?
3 hours of play = 120 hands total = N
Assume only first 3 listed events are what you are interested in since the chance of getting at least one of all of the listed Lucky Lucky events in 120 hands is nearly 100%:
p = 0.000016+0.000172+0.000388 = 0.000576
P(LL=0) = (1 - p)^N
= (1 - 0.000576)^120
= 93.3% chance of not getting a Lucky Lucky in 120 hands
P(LL>0) = 1 - P(LL=0)
= 6.7% chance of getting at least one Lucky Lucky in 120 hands
= 0.00030%
Blackjack Lucky Lucky Odds
The chances of getting those 3 events to occur exactly (no more no less) in 120 hands is p = (0.000172)^2 (0.000388) (0.999424)^117 COMBIN(120,3)
= 0.00030%
I think you are missing a *3 in there. combin(120,3) ways for the 3 events, but they can be in 3 different orders.
Assume average 40 hands dealt per hour
3 hours of play = 120 hands total = N
Assume only first 3 listed events are what you are interested in since the chance of getting at least one of all of the listed Lucky Lucky events in 120 hands is nearly 100%:
p = 0.000016+0.000172+0.000388 = 0.000576
This probability is the chance of getting any of the following: suited 777, unsuited 777, suited 678
p(0 wins) = (1-0.000576)^120 = 0.933196104
p(1 win) = (1-0.000576)^119 * 0.000576^1 * combin(120,1) = 0.06453969
Blackjack Lucky Lucky Odds
p(2 wins) = (1-0.000576)^118 * 0.000576^2 * combin(120,2) = 0.002213179
p(3 or more wins) = 1 - p(0 wins) - p(1 win) - p(2 wins) = 5.10279E-05 = 0.0051%
Indeed, very lucky; nearly a 1 in 20,000 chance of getting 3 or more of the wins listed above.
I think you are missing a *3 in there. combin(120,3) ways for the 3 events, but they can be in 3 different orders.
COMBIN(120,3) = 120! / 3!(120-3)! = 280,840 possible combinations should also take into account 3 different orders.
Its good that you were alert to how many people were at the table since you are playing at under or over the assumed rate of play depending upon number of players and number of them who were taking advantage of the side bets available to them.
If you are playing slower than the Rate of Comps that is marginally good for you.
COMBIN(120,3) = 120! / 3!(120-3)! = 280,840 possible combinations should also take into account 3 different orders.
Actually, miplet is right.
You have one set of 2 matching items and 1 unique item. To use the combin function, it should be combin(120,2)*combin(118,1), which is identical to combin(120,3)*3.